Abstract
Modeling the location of cellular Base Stations(BS) have two fundamental directions. Traditionally, BS sites
have been modeled by hexagonal grid-based topology. But in reality, BS deployments are irregular and random depending
on planning, opportunistic placement and many other topological and demographic factors. Hence,
random spatial models have become increasingly popular for the abstration of the BS distributions.Using the
tools from stochastic geometry, it is possible to analytically evaluate the key performance metrics such as
coverage (outage) probability and data rate. In most works, locations of the BSs are modeled as homogeneous Poisson point process (PPP).
Although PPP provides tractable results, it is simple and idealized model as the locations of the BSs are assumed to be
mutually independent. However, in reality macro BSs are installed after a certain distance and thus the neighbouring nodes in the underlying point process
should have some "repulsion".
On the other hand, more small cell BSs are deployed to serve the users in densly populated areas with high capacity demand. Hence, the small cell distribution has a clustering nature which is correlated to the user distribution. With recent proposal of Strauss and Geyer Saturation process which are two variant of Gibbs process to model replusive and clustering patterns of BS deployments. The project, investigates the applicability of these proposed point process by testing in a contemporary released BS site-map of London.
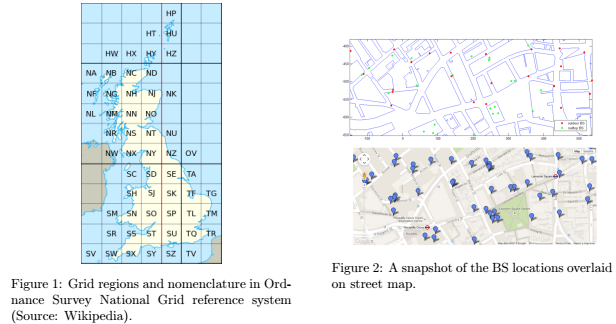
Input Data

Procedure
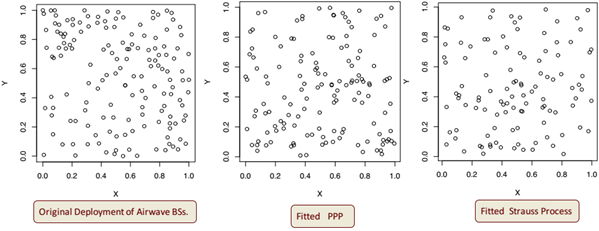
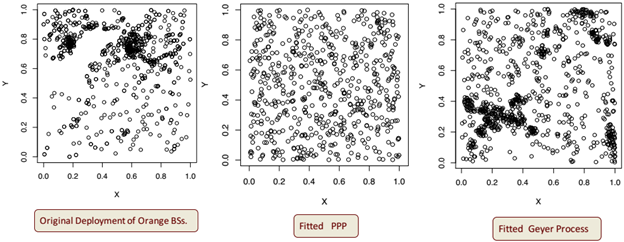
• Choose a specific area of London and generate 2D coordinates of the BS locations of different mobile operators like Airwave, Orange from the dataset.• Fit the Strauss and Geyer saturation process using spatstat package in R.
• Generate realizations of the point patterns with the parameter values obtained from the fitting.
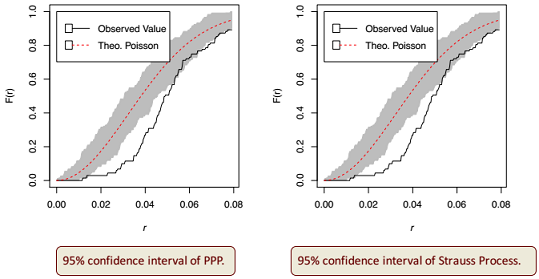
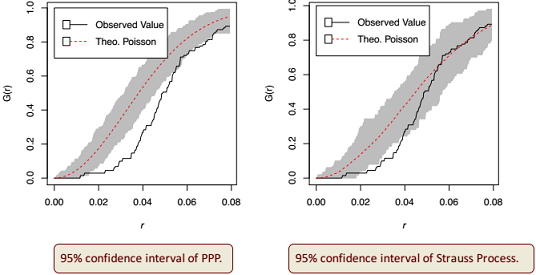
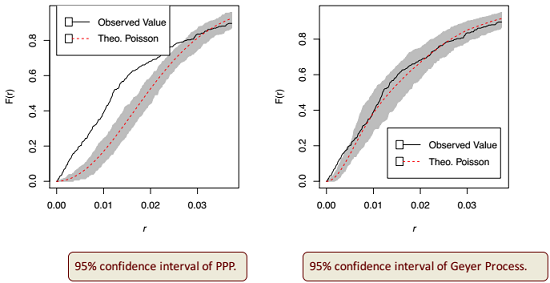
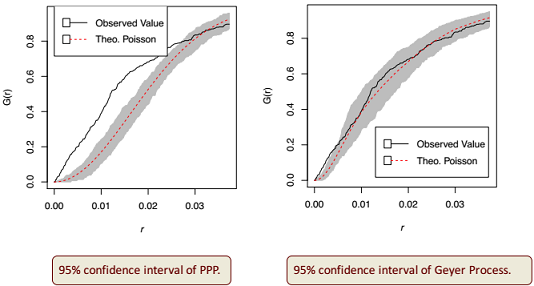
• Test the hypothesis that the deployments of the BSs are realizations of either of two poisson processes using metrices like F-function,G-function
Results
- For BS deployment exhibiting inhibition, PPP is a good fit. But, Strauss process exhibits better fitness.
- For BS deployment with clustering, Geyer saturation process has better fitting to the data compared to PPP.
Reference
- • J. Andrews, F. Baccelli, and R. Ganti, "A tractable approach to coverage and rate in cellular networks," IEEE Transactions on Communications, vol. 59, no. 11, pp. 3122-3134, Nov.2011.
- • H. ElSawy, E. Hossain, and M. Haenggi, "Stochastic geometry for modeling, analysis, and design of multi-tier and cognitive cellular wireless networks: A survey," IEEE Communications Surveys and Tutorials, vol. 15, no. 3, pp. 996-1019, 2013.