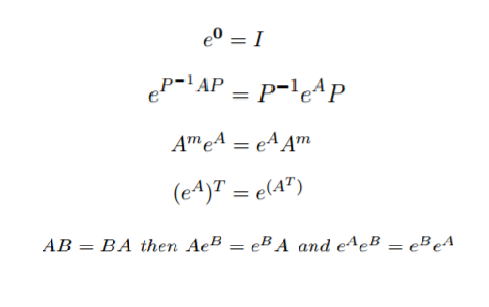
Abstract
With expanding social networks and large online social data, large graphical representations of useful data are getting prevalent.
A lot of graph mining tasks exist which when run on graphs extract useful information. But with the growing graph size, issues like
scalability and computational cost of these tasks arise. So, here in this project we explore usefulness of exponential of graph
matrices to observe any interesting properties. Here, we explore Eigen Vector decomposition properties on exponential matrix.
In addition, several important mathematical properties relevant to graph mining which can be modelled using exponential of a matrix
have been discussed. Specifically, we aim at improving Clustering and Link Prediction algorithms using mathematical intuition
obtained from exponential of a matrix.
Background
Exponential of Matrix
Exponential of a matrix is a matrix function defined on a square matrix. Exponential of a matrix can be computed using power series given by:
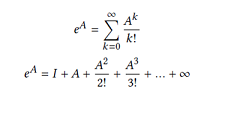
For any matrix A, the above power series converges (for matrix with finite norm) and hence exponential of a matrix is well defined. In case of graphs, we represent graph using an n x n adjacency matrix, where n is the number of nodes. Hence, matrix exponential is computed on adjacency matrix.
Exponential Features
Exponential of a matrix could be used to model certain useful features which can be used in Graph Mining Tasks.
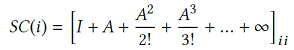
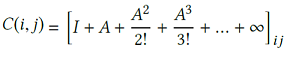
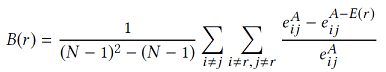
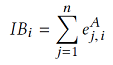
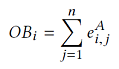
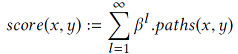
Eigen Decomposition and Clustering
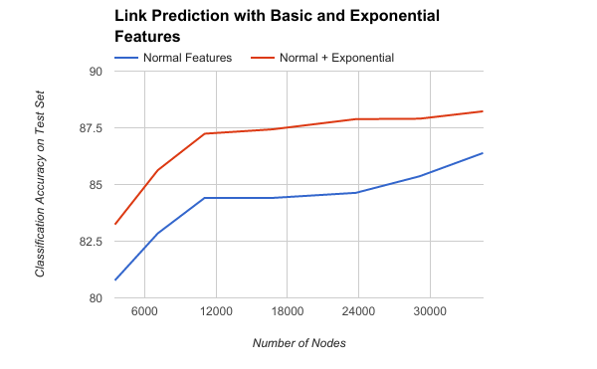
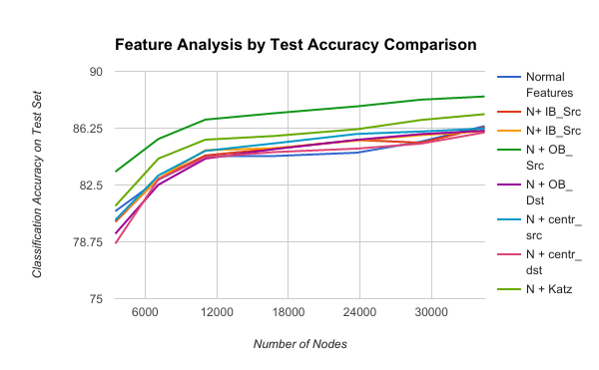
Link Prediction
Procedure
Several directed and undirected datasets from SNAP Dataset Collection were used for our experiments.
- Data Preprocessing – Adjacency matrix has been constructed out of edge data of graph.
- Exponential Features – Exponential of the matrix has been computed and features have been extracted for Link Prediction.
- Training and Test Sets – We have sampled equal number of edge and non-edge node pairs for classification. Further, a 80-20 split is considered to build training and test sets.
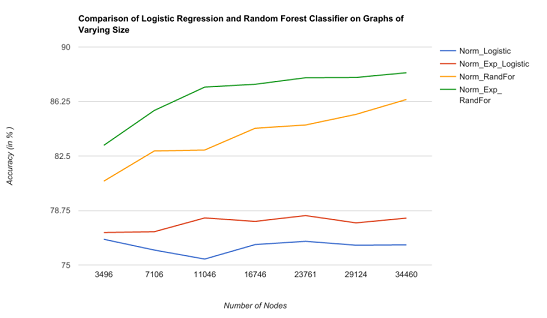
- Classifiers –Various classifiers such as Random Forest, Logistic Regression, Support Vector Machine, and Neural Networks have ben used for Edge Classification task.
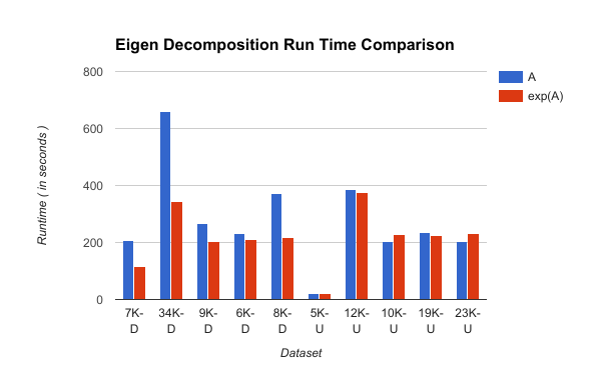
Results
Reference
- • M. Benzi, E. Estrada, and C. Klymko, "Ranking hubs and authorities using matrix functions," Linear Algebra and its Applications 438, 5(2013), 2447-2474
- • E. Estrada, and N. Hatano, "Communicability in complex networks," Physical Review E 77, 3(2008), 036111.